概述
本文主要介绍红黑树原理,以及应用范围。
什么是二叉树
二叉查找树(BST),其特性为左分支小,右分支大,且左右子树都为二叉排序树,二叉树这里不再累述。
看一次二叉树的插入操作,假设初始二叉树为图一(初始数据8 9 12)
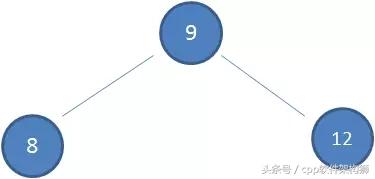
现在插入数据(7 6 5 4 3)
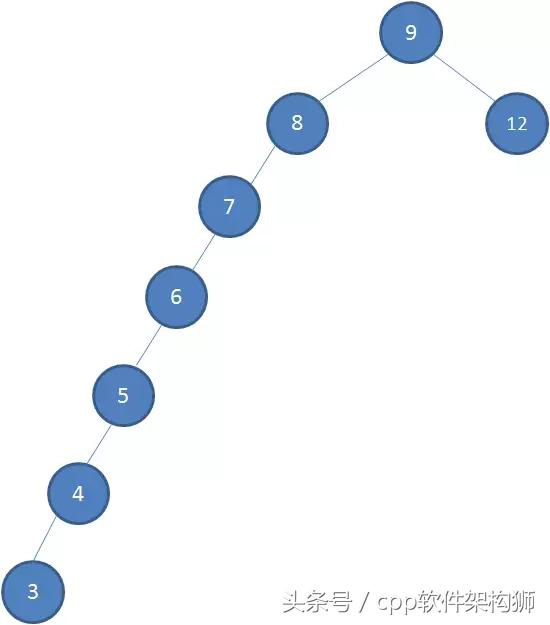
可以看到其左分支的深度在不断增加,查询的时候几乎和线性查询没有区别,比正常的二叉树查询性能降低了很多,这就需要引入红黑树来解决这种多次插入新节点而引起的不平衡.
什么是红黑树
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树有什么好处
红黑树的五条规则保证了其最长路径不超过最短路径的两倍,这样便不会出现之前的二叉树线性问题了,大大提高了二叉树查询检索的效率.
一个典型的红黑树
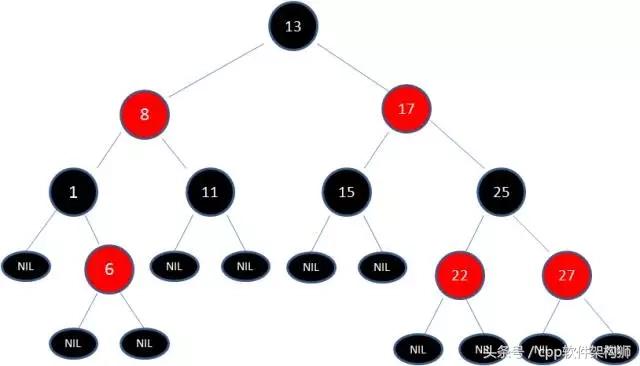
红黑树特性
红黑树的特性:
(1)根节点是黑色。
(2)每个节点或者是黑色,或者是红色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
红黑树的应用
定理:一棵含有n个节点的红黑树的高度至多为2log(n+1), 即 h <= 2log(n+1),2作为常数,log的底数对其影响更大,则忽略常数2和 1,其时间复杂度为O(log n).
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(Log n),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,,都是通过红黑树去实现的,JDK8 hashmap的链表也用了红黑树。
红黑树插入新节点
试着插入为值为14的新节点,由于父节点为15且是黑色节点,这并没有破坏红黑树的结构,不需要做出任何的改变.
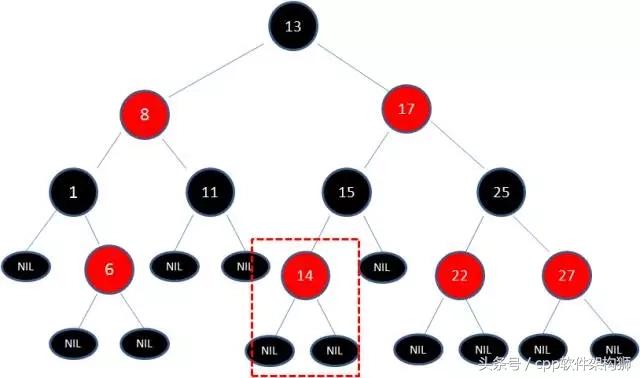
再来看如果插入的值是21的新节点,可以看到由于原来的父节点22是红色的,21节点也是红色,这打破了红黑树规则4(即:红节点的子节点全为黑),所以需要对红黑树进行调整,调整有两种方式,change color 和左右旋转.
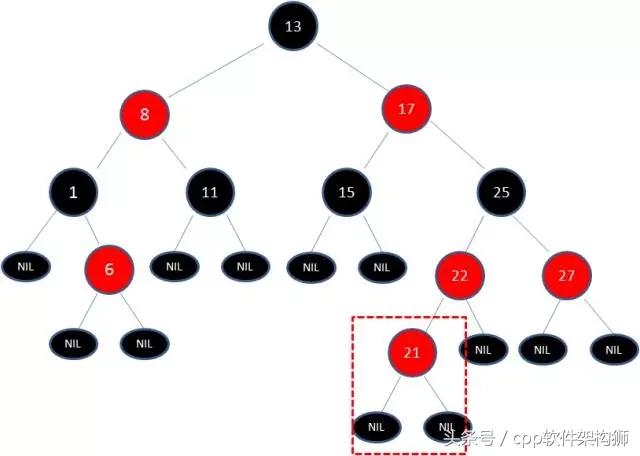
红黑树再平衡-CHANGE COLOR
为了让新插入后的红黑树符合规则,会采取对节点红变黑或者黑变红的方式,下面介绍上面的插入21时候的变色方式。

第一步:其中25不是根节点,21-22 连续红色,不满足规则4(即:红节点的子节点全为黑),但由于21子节点已经是黑色NIL,无法改变颜色了,所以需要把22红变黑来满足规则4。
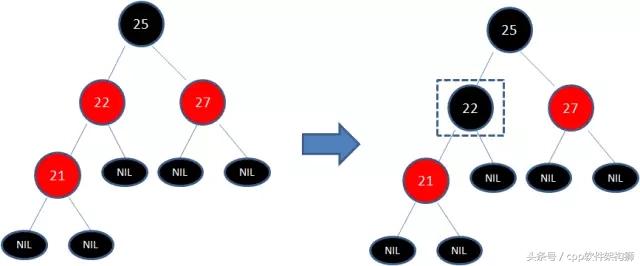
第二步:变色后又不符合规则5(即:一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点),明显的25-22-NIL出现了3个黑色节点,大于了25-27-NIL的两个黑色节点,所以需要把25节点也变成红色,来满足规则5。
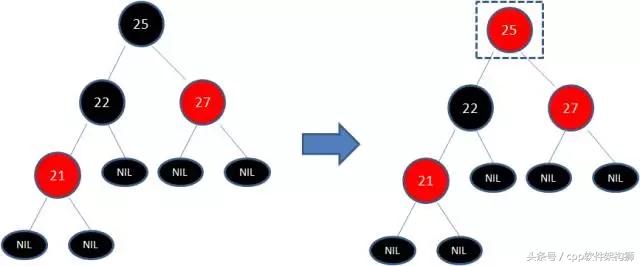
第三步: 25变成红色后,由于25-27又是连续红色,同理继续将27变为黑色,这样通过多次变色便后,新插入的部分数据终于满足了红黑树的规则,成为一个新的红黑树,剩余的再平衡由左右旋来解决。
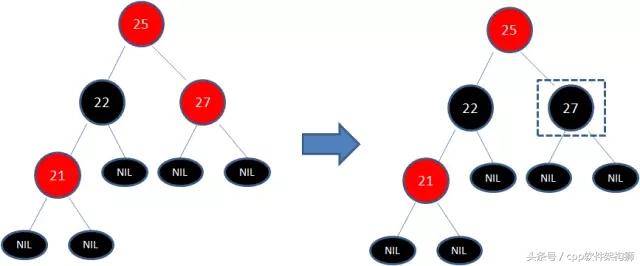
红黑树再平衡-左右旋转
左旋之篡位
有一个boss,有左右副手,左右副手也都有左右下级,假设右边的级别比左边高,右边在同级中排第一,左边排第二。
有一天boss右副手篡位了,带着他的下级升级,原来的右副手的右副手,跳级提升为现在的右副手,而原来的右副手的左副手同级提升,升级为原来boss的右副手
瘦死的骆驼比马大,原来的boss虽然变为了左副手,但他还是管着篡位者的左副手的,原来的boss的下级就比较惨了,跟着boss待在地位比较低下的BOSS的左边。[右旋之篡位可以思考一下,和左旋是同一个道理,参照变成了左边的权利比右边权利高而已]
篡权方变化:
原右副手-篡权者 >>> 现在的boss >>>跳一级
原右副手的右副手 >>> 现在的boss的右副手 >>>跳一级
原右副手的左副手 >>> 现在左副手的右副手(即:原boss的右副手)>>>同级提升
可怜方变化:
原boss-可怜人 》》》 现在boss的左副手 》》》降一级
原boss的左副手 》》》 现在左副手的左副手(即:原来boss的左副手)》》》降一级之后,还被同级下降,祸不单行。
左旋
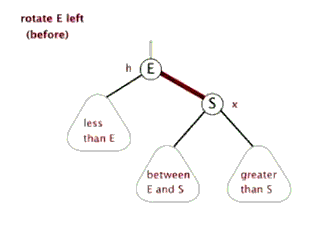
逆时针旋转两个节点,使得父节点被自己的右孩子取代,而自己却成为了自己的左孩子,我的理解是降级为左,升级为右,右边权力高,即降了一个等级,自己被右副手取代,但是原来的右副手的左下级和你的左副手还是归你管。
再明白点儿就是,右副手抢了你的位置,你和你原来你的左副手都降了一级,而右副手和右副手的左右副手都升了一级。
再简明一点儿就是右副手篡位了,他的下级都升级了(右下级升一级,左下级同级提升为右副手),而原来的BOSS和他的手下都降了一级或更多级,这样应该比较好理解,图中的ABC可以看成一些隐藏的二叉树,并不代表值为 a b c.
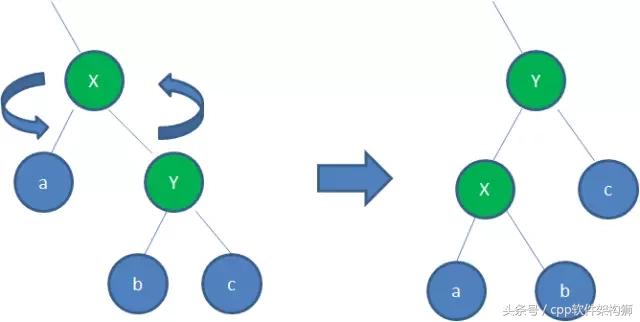
还有一种理解方式,那就是平面左旋,即X Y a b c 都按逆时针旋转90度.

右旋
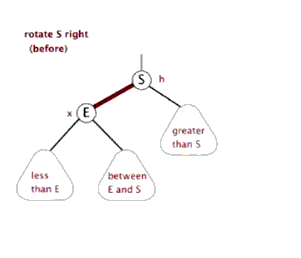
顺时针旋转X Y 节点使得父节点被左孩子取代,而自己成为自己的右孩子,我的理解是降级为右,升级为左,左边权力高,即降了一个等级,自己被左副手取代,但是原来的左副手的下级(左副手的右副手)和你的右副手还是归你管。
再明白点儿就是,左副手抢了你的位置,你和你原来的右副手都降了一级或更多级,而左副手和左副手的左右副手都升了一级。
再简明一点儿就是左副手篡位了,他的下级都升级了(左下级升一级,右下级同级提升为左副手),而原来的BOSS和他的手下都降了一级或者更多级,这样应该比较好理解,图中的ABC可以看成一些隐藏的二叉树,并不代表值为 a b c.
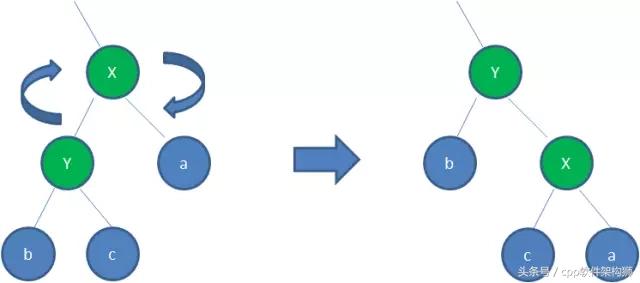
还有一种理解方式,那就是平面右旋,即X Y a b c 都按顺时针旋转90度,交换位置.

红黑树的插入与调整
因为要满足红黑树的这五条性质,如果我们插入的是黑色节点,那就违反了性质五,需要进行大规模调整;
如果我们插入的是红色节点,那就只有在要插入节点的父节点也是红色的时候违反性质四或者当插入的节点是根节点时,违反性质二。
所以,我们把要插入的节点的颜色变成红色。
不需要调整
1、当插入的节点是根节点时,直接涂黑即可;
2、当要插入的节点的父节点是黑色的时候,这个时候插入一个红色的节点并没有对这五个性质产生破坏,所以直接插入不用在进行调整操作。
需要调整
即插入节点的父结点也是红色。
因为左右对称的缘故,在此只讨论父结点P位于祖父节点G的左支LEFT的情况(N 为插入节点):
1 叔叔节点是红色,
这时候只进行换色操作:将父结点和叔叔节点涂成黑色,祖父节点涂成红色,P U >>> BLACK ,G >>> RED。
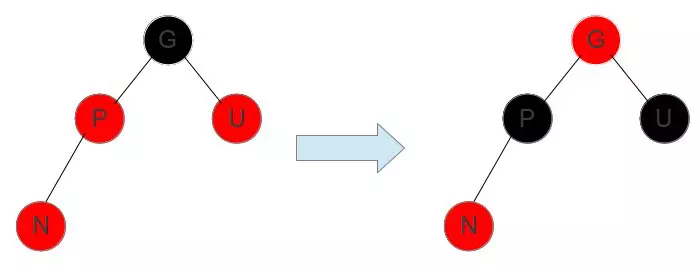
2 叔叔节点U是黑色,插入节点N位于父节点的右支
这时候需要将父结点P当成新的插入节点,并以P为支点进行左旋操作(P G连线断开,绕一圈连接到N,N左旋一圈,连接到G),P >>> LEFT,然后和情况三一样处理。
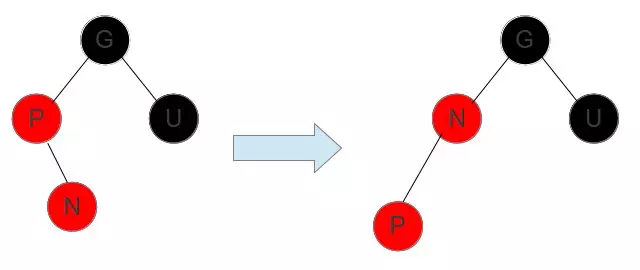
3 叔叔节点U是黑色,插入节点N位于父结点P的左支
这时候需要先进行换色操作:将父结点涂成黑色,祖父节点涂成红色,然后进行右旋操作。P >>> BLACK,G >>> RED, G >>> RIGHT。
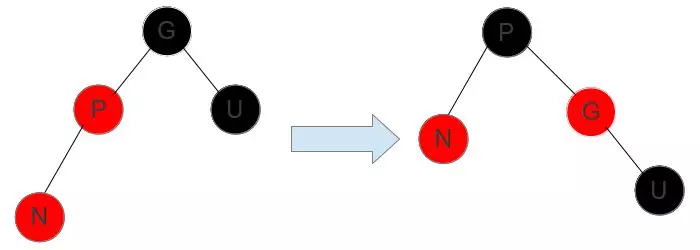
红黑树的删除与调整
如果被删除结点有孩子,则需要选一个合适的孩子节点作为新的根节点,称为当前节点。
1、只有左孩子或只有右孩子,则让该孩子作为当前节点替代被删除结点;
2、左右孩子均存在,则用被删除结点的中序后继结点作为当前节点替代被删除结点。
注意:替代只是值的互换,颜色不变。
即:当前节点是黑色,被删除结点是红色。替换后,当前节点位于被删除结点的位置,是红色;被删除结点位于当前节点原来的位置,是黑色。
不需要调整的情况:
1、被删除结点的是红色的。
2、被删除结点只有一个孩子,用孩子的值替换被删除节点,删除孩子结点。
需要调整的情况:(被删除节点为黑色)
因为左右对称的缘故,在此只讨论父结点位于祖父节点的左支的情况:
1、兄弟节点为红色
这时候需要互换父结点和兄弟节点的颜色,并进行左旋操作。P B 互换颜色 > LEFT
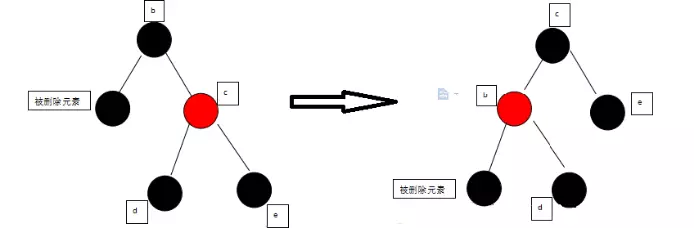
2、兄弟节点为黑色,且其左右孩子也为黑色
将兄弟节点涂成红色,再将父结点当成新的被删除结点(只是当成,并不删除)进行一次调整(右图中少了根节点的左孩子被删除元素)。B 变红 ,P 当成新的删除节点
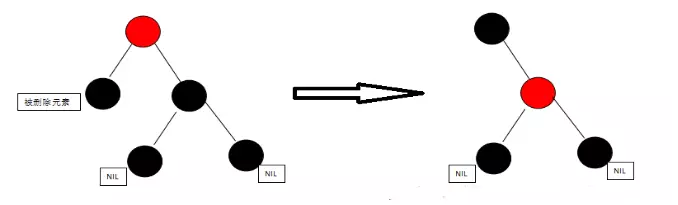
3、兄弟节点为黑色,且其左孩子为红色
先换色:左孩子涂成黑色,兄弟节点涂成红色;再以兄弟节点为支点右旋(b和a连线断开,右旋到c和c连接,c右旋到a和a连接)。变成情况4 B-L变黑,B变红,再以B RIGHT >>> 情况4
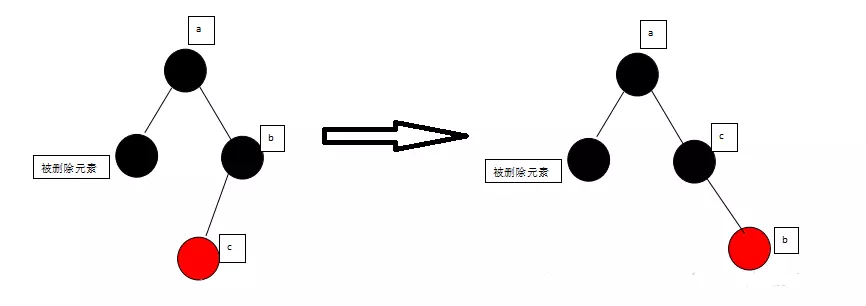
4、兄弟节点为黑色,且其右孩子为红色
先换色:父结点的颜色赋给兄弟节点,父结点涂成黑色,兄弟节点的右孩子涂成黑色;再左旋(右图中a 的左孩子是被删除元素)。P-C > B-C ,P >BLACK,B-R > BLACK >>>LEFT
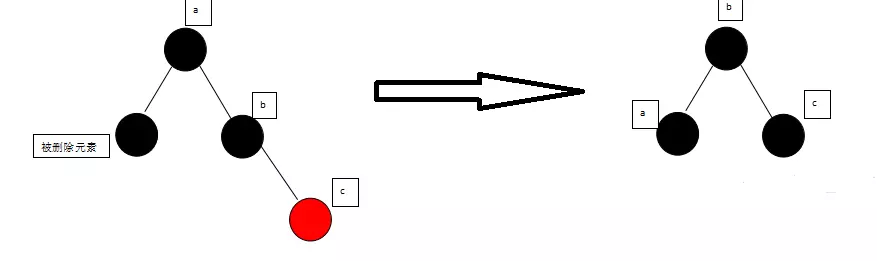
左右旋的使用
以刚才插入21节点时为栗子,我们知道经过变色后,成了下面的模样。
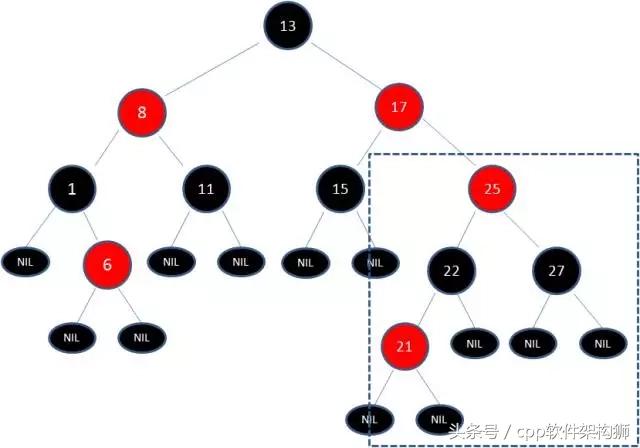
此时出现一个问题,节点17-25都为红色,这违背了规则4(即:红节点的子节点都为黑),试一下把17变为黑色,这又违背了规则5(即:从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点)。
因为17变黑后,13-17-15-NIL 全为黑4个黑色 大于了13-8-11-NIL的三个黑色,更加不可能把根节点13变为红色了,单靠CHANGE COLOR已经无法解决问题了。
需要用到旋转来解决,先试一下把13当X,17当Y,我们先来左旋try一下,得到下图初始结果,为什么左旋而不是右旋呢,明显的图中,左边部分太过突出了,突出了就需要被旋转一下。
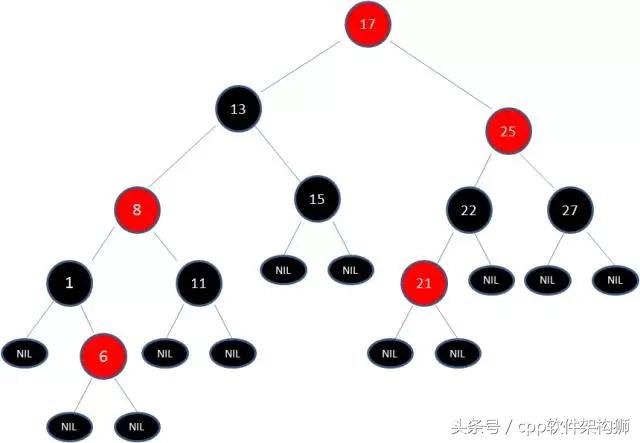
此时根节点为17,是红色的,根据规则1(即:根节点必须为黑色),需要变为黑色,其他节点根据规则变色,得到下图的结果。
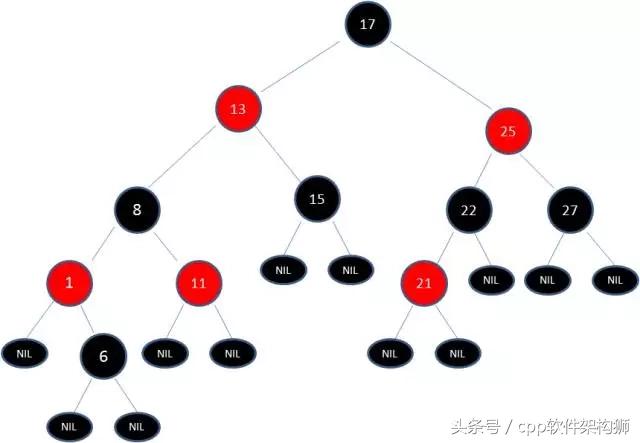
但此时仍然有一个问题,就是根据规则5(即:从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点),明显此时17-13-8-1-6-NIL包括了4个黑色节点,而其他路径中,比如17-13-15-NIL只存在三个黑色节点,此时又需要旋转。
再Try一下右旋,将13作X 8作Y进行右旋,得到如下的结果,为什么右旋而不是左旋呢,明显的图中,左边部分太过突出了,突出了就需要被旋转一下。
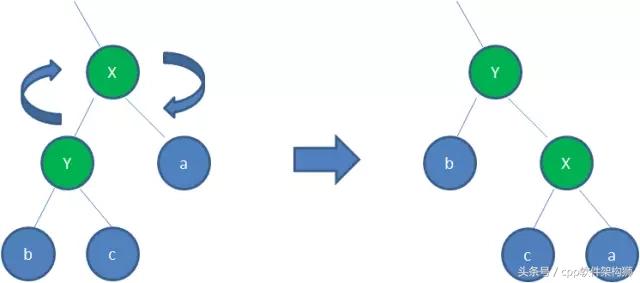
但是还有些节点颜色不对,根据规则4(即:红节点的子节点全为黑色),需要对相应的节点进行变色,达到规范,最终形成如下的新平衡红黑树。
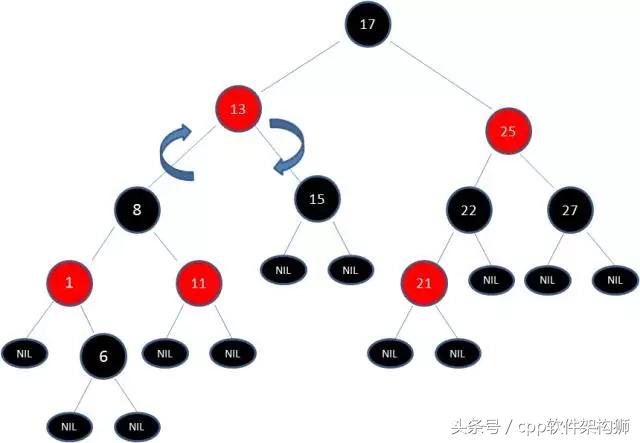
为什么需要再平衡
通过上诉说明,我们可以看出,在新插入数据的时候,对红黑树的再平衡过程是比较复杂的,如此复杂的再平衡目的为何,其实是为了满足红黑树规则,让红黑树具备快速查找的能力,而不是像普通二叉树一样在线性数据插入时候造成性能问题。
再平衡规则
从上图中的左右两次旋转可以看到,在变色无法处理的情况下,不管左旋还是右旋都是有规律的,其目的就是让红黑树尽量小的线性延伸,尽量缩短查找时需要访问的节点深度,简明点儿说,谁突出,谁挨打,用一个成语解释叫首当其冲。
总结
此文不介绍红黑树的实现,只介绍其性质和原理、应用,以及和普通二叉树的区别。
一盏灯, 一片昏黄; 一简书, 一杯淡茶。 守着那一份淡定, 品读属于自己的寂寞。 保持淡定, 才能欣赏到最美丽的风景! 保持淡定, 人生从此不再寂寞。




